Data Structures: Binary Search Tree
Type of Data Manipulation
木構造は、Data Structureのうち再帰的構造をもつ.
- Iterative 反復的
- Recursive 再帰的・帰納的 pythonでは重い
Data Manipulation Speed
| Query | Linked list | Array normal | Array sorted | BST |
|---|---|---|---|---|
| SEARCH | O(n) | O(n) | O(logn) | O(logn) |
| INSERT | O(1) | O(1) | O(n) | O(logn) |
| REMOVE | O(n) | O(n) | O(n) | O(logn) |
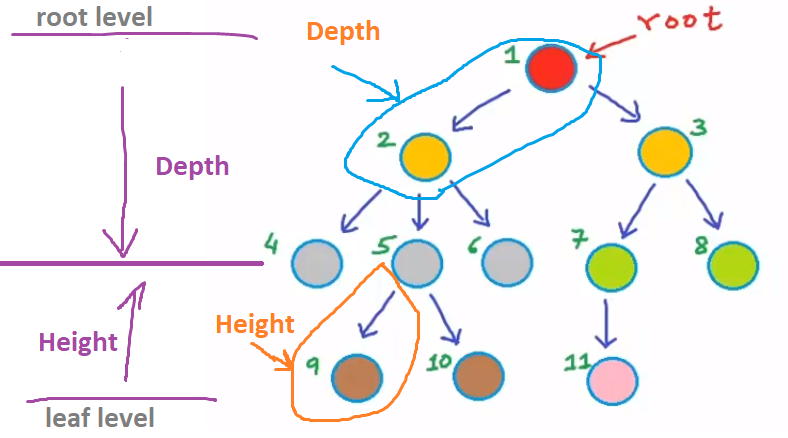
Keys of Tree
- Queries
- 追加 insert()
- 削除 remove()
- 検索 search()
- 更新 update()
- Parts of Tree
- Root
- Node
- Leaf
- parent
- child
- Pros/Constructive
- 重複は許されない
- 検索と更新に優れている
Code for Trees
以下二つのクラスを用意する.
- 二分探索木におけるノードの構造を表現するクラス
-
二分探索木の構造や処理を表現するクラス
- Node: 二分探索木におけるノードの構造を表現するクラス
# 左の子孫の値 ≤ 親の値 ≤ 右の子孫の値
class Node():
# Attribution * 3
def __init__(self, val):
self.value = val
self.leftChild = None
self.rightChild = None
# 追加
def insert(self, data):
# 探索木で重複は許されない
if self.value == data:
return False
# Nodeより値が小さい時
elif self.value > data:
# すでに左子ノードが存在する場合は更新
if self.leftChild:
return self.leftChild.insert(data)
# 左子ノードが存在しない場合は新規作成
else:
self.leftChild = Node(data)
return True
# Nodeより値が大きい時
else:
# すでに右子ノードが存在する場合は更新
if self.rightChild:
return self.rightChild.insert(data)
# 右子ノードが存在しない場合は新規作成
else:
self.rightChild = Node(data)
return True
# 検索
def find(self, data):
# クエリの値とマッチしたらTrue
if(self.value == data):
return True
# クエリの値がノードの値より小さい時 -> 左
elif self.value > data:
# すでに左子ノードが存在する場合は更新
if self.leftChild == True:
return self.leftChild.find(data)
# 左子ノードが存在しないLeafの場合はFalse
else:
return False
# クエリの値がノードの値より小さい時 -> 右
else:
# すでに右子ノードが存在する場合は更新
if self.rightChild:
return self.rightChild.find(data)
# 右子ノードが存在しないLeafの場合はFalse
else:
return False
# 高さ(エッジ数)を計る関数
def getHeight(self):
if self.leftChild and self.rightChild:
return 1 + max(self.leftChild.getHeight(), self.rightChild.getHeight())
elif self.leftChild:
return 1 + self.leftChild.getHeight()
elif self.rightChild:
return 1 + self.rightChild.getHeight()
else:
return 1
# 関数
def preorder(self):
if self:
print (str(self.value))
if self.leftChild:
self.leftChild.preorder()
if self.rightChild:
self.rightChild.preorder()
def postorder(self):
if self:
if self.leftChild:
self.leftChild.postorder()
if self.rightChild:
self.rightChild.postorder()
print (str(self.value))
def inorder(self):
if self:
if self.leftChild:
self.leftChild.inorder()
print (str(self.value))
if self.rightChild:
self.rightChild.inorder()
- Tree: 二分探索木の構造や処理を表現するクラス
class Tree:
# 木の初期化
def __init__(self):
self.root = None
# 追加
def insert(self, data):
# 更新
if self.root:
return self.root.insert(data)
# 追加
else:
self.root = Node(data)
return True
def find(self, data):
# Rootから
if self.root:
return self.root.find(data)
else:
return False
def getHeight(self):
if self.root:
return self.root.getHeight()
else:
return -1
#削除
def remove(self, data):
# empty tree
if self.root is None:
return False
# data is in root node
elif self.root.value == data:
if self.root.leftChild is None and self.root.rightChild is None:
self.root = None
elif self.root.leftChild and self.root.rightChild is None:
self.root = self.root.leftChild
elif self.root.leftChild is None and self.root.rightChild:
self.root = self.root.rightChild
elif self.root.leftChild and self.root.rightChild:
delNodeParent = self.root
delNode = self.root.rightChild
while delNode.leftChild:
delNodeParent = delNode
delNode = delNode.leftChild
self.root.value = delNode.value
if delNode.rightChild:
if delNodeParent.value > delNode.value:
delNodeParent.leftChild = delNode.rightChild
elif delNodeParent.value < delNode.value:
delNodeParent.rightChild = delNode.rightChild
else:
if delNode.value < delNodeParent.value:
delNodeParent.leftChild = None
else:
delNodeParent.rightChild = None
return True
parent = None
node = self.root
# find node to remove
while node and node.value != data:
parent = node
if data < node.value:
node = node.leftChild
elif data > node.value:
node = node.rightChild
# case 1: data not found
if node is None or node.value != data:
return False
# case 2: remove-node has no children
elif node.leftChild is None and node.rightChild is None:
if data < parent.value:
parent.leftChild = None
else:
parent.rightChild = None
return True
# case 3: remove-node has left child only
elif node.leftChild and node.rightChild is None:
if data < parent.value:
parent.leftChild = node.leftChild
else:
parent.rightChild = node.leftChild
return True
# case 4: remove-node has right child only
elif node.leftChild is None and node.rightChild:
if data < parent.value:
parent.leftChild = node.rightChild
else:
parent.rightChild = node.rightChild
return True
# case 5: remove-node has left and right children
else:
delNodeParent = node
delNode = node.rightChild
while delNode.leftChild:
delNodeParent = delNode
delNode = delNode.leftChild
node.value = delNode.value
if delNode.rightChild:
if delNodeParent.value > delNode.value:
delNodeParent.leftChild = delNode.rightChild
elif delNodeParent.value < delNode.value:
delNodeParent.rightChild = delNode.rightChild
else:
if delNode.value < delNodeParent.value:
delNodeParent.leftChild = None
else:
delNodeParent.rightChild = None
def preorder(self):
if self.root is not None:
print("PreOrder")
self.root.preorder()
def postorder(self):
if self.root is not None:
print("PostOrder")
self.root.postorder()
def inorder(self):
if self.root is not None:
print("InOrder")
self.root.inorder()

Leave a Comment