随時更新中

Ronald A. Fisher, father of modern statistics, enjoying his pipe.

The 5 Basic Statistics Concepts Data Scientists Need to Know

1. Statistical Features 記述統計
2. Probability Distributions 確率分布
3. Dimensionality Reduction 次元削除
4. Over and Under Sampling 標本サイズ、区間推定
5. Bayesian Statistics ベイズ統計

重要な統計学カテゴリ

1. 記述統計学と基礎統計
2. 確率分布
3. 推測的統計 from 推測統計学
4. 仮説検定 from 推測統計学
5. ベイズ統計学
6. Advanced Stats

トピック

1. 記述統計学と基礎統計

- 統計学の全体感
- 記述統計指標まとめ
- 標準偏差と分散
- 統計的前処理
- 多重共線性
- 最小二乗法
- 損失関数
- 離散型と連続型データ
- 統計学とグラフ（箱ひげとヒストグラム, 散布図）

2. 確率分布

- Population and Sample
- 正規分布
- 確率分布の種類: 二項分布、多項分布、連続一様分布、T分布
- 確率と面積: 率確率密度関数(PDF)
- 中心極限定理

3. 推測的統計 from 推測統計学

- 推定（estimation）と推論（inference）
- Bias vs. Variance
- 最尤推定 vs. MAP推定
- 信頼区間と区間推定
- パラメータとバイアス
- 推量と推定

4. 仮説検定 from 推測統計学

- 有意水準と帰無仮説
- T検定とZ検定
- パラメトリック検定 vs. ノンパラメトリック検定

5. ベイズ統計学

- ベイズの定理

6. Advanced Topic

- 次元削除
- 正則化
- 時系列データにおける統計学
- 交差エントロピー誤差

1. 記述統計学と基礎統計

統計学の全体感

1. 記述統計学（データの要約値・可視化）
2. 推測統計学(モデル作成)
   • 統計的推定（）
   • 仮説検定（信頼区間、P値、t検定）
3. ベイズ統計学

記述統計指標まとめ

データの要約値

• 平均値: すべての数値を足して、数値の個数で割った値
• 中央値: 数値を小さい方から並べたときに、真ん中に来る値
• 最頻値: 一番個数が多い値
• 標準偏差: データの散らばりの度合いを示す値
• 回帰: 独立変数間の関係性を表す

使い分け 　正規分布の場合は「平均値」. 年収など正規分布しない場合は「中央値」.

標準偏差と分散

分散 = 標準偏差 ** 2

統計的前処理

• 欠損値処理(Missing Data)
• 外れ値処理(Outlier Detection)
• ダミー変数(Dummies): 男女->01
• 連続値の離散化(Sampling): 10代,20代,30代,40代,50代->0,1,2,3,4
• 対数処理: 対数正規分布
• 多重共線性*

多重共線性 Multicollinearity

説明変数間で相関係数が高いときに、それが原因で発生する現象

問題点

• 分析結果の係数の標準誤差が過剰に大きくなる
• 決定係数が過剰に大きくなる
• 回帰係数の符号が逆になる（+->-）
• T値が小さくなる

最小二乗法

最小二乗法 ＝ 等分散ガウス分布 ＋ 最尤推定 通常の最小二乗法は、二乗残差の合計を最小化すること. 具体的にはは、データを通る回帰直線が与えられたら、各データポイントから回帰直線までの距離を計算し、それを二乗し、二乗した誤差をすべて合計する.

損失関数（誤差関数）

モデルと測定値の誤差を表す関数のこと

離散型データと連続型データ

• 離散型データ
  • １つ１つの値が独立しているデータ
  • 例: サイコロの目, 人数
• 連続型データ
  • ある数値から別の数値までの間に無限に数値が存在するデータ
  • 例: 身長, 体重

統計学とグラフ（箱ひげとヒストグラム, 散布図）

箱ひげ図

引用元：wikipedia

グラフかわかること.

• 中央値
• 最小値と最大値
• 外れ値
• 四分位数
• 四分位範囲（箱の上辺・底辺間の範囲: 第1四分位数と第3四分位数の間の範囲）

ヒストグラム

引用元：Peltier Tech Blog

グラフかわかること.

• データの分布の全体感

散布図

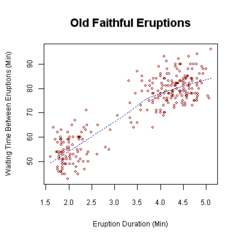
引用元：wikipedia

グラフかわかること.

• 2つの独立変数感の相関関係の強さ（正・負の相関）

2. 確率分布

Population and Sample

• 母集団とサンプル（無作為抽出と確率）

• 未来のデータを含む全データと過去のデータ（未来のデータは未知・確率的）

• データの分布が分かれば
• 発生確率が分かれば
• 予測可能になる
• あとは異なる変数間の関係だけを調べろ

正規分布

• 正規分布を知れば「その発生確率を計算できる現象」がグッと増えてくるということ

• 正規分布とはランダムな分布、未知なものに仮定

• 正規分布を前提にしている. Why?
  • 自然界のデータによく存在する
  • 中心極限定理
  • シンプルに解釈できる

席分布の特徴は、

• 平均値と最頻値と中央値が一致*する。
• 平均値を中心にして左右対称である。（直線# x=μに関して対称）
• 分散（標準偏差）が大きくなると、曲線の山は低くなり、左右に広がって平らになる。分散（標準偏差）が小さくなると、山は高くなり、よりとんがった形になる。

確率分布の種類: 二項分布、多項分布、連続一様分布、T分布

• 二項分布（独立離散確率分布）
• サンプル数が多いと正規分布になるよ

確率と面積: 確率密度関数(PDF)

　データ（各特徴における各確率変数）の出現確率を数式かしたもの. その範囲にわたって確率密度関数を積分することにより得ることができるよう定義される 　

• 確率変数
  • 離散型
  • 連続型
    • 確率密度関数(確率=面積)
      • 確率変数
      • 確率分布

追記：確率密度を積分すると、確率になる

中心極限定理と対数の定理

　複数の変数の分布が正規分布に近づく

3. 推測的統計 from 推測統計学

推定（estimation）と推論（inference）

• 推定はある特定の値を何らかの方法で求めること
• 推論は確率計算によりある確率分布を求めること

推量と推定

• 推定
  • 点推定
  • 区間推定

Bias vs. Variance Trade-Off

精度の高いモデルとはバイアスと分散を共に低く抑えられた時、初めて達成されるものである. 正確なモデルを構築するだけでなく、過剰適合と不足適合の間違いを避けるために大切.

損失関数における誤差 = Bias + Variance + Noise*

Bias: バイアスは、モデルの平均予測値と予測しようとしている正しい値の差です。

バイアスとは

バイアスは、モデルの平均予測値と予測しようとしている正しい値の差. バイアスが高いモデルは、トレーニングデータにほとんど注意を払わず、モデルを単純化し過ぎてしまう. それは常にトレーニングとテストデータに高い誤差をもたらす.

• 低バイアス：ターゲット関数の形式に関する仮定を少なくす.
• 高バイアス：ターゲット関数の形式についてより多くの仮定を提案する.

分散とは

分散は、与えられたデータポイントに対するモデル予測の変動性、またはデータの広がりを示す値. 分散が大きいモデルはトレーニングデータに多くの注意を払い、それまで見たことのないデータを一般化しない. その結果、このようなモデルはトレーニングデータでは非常によく機能するが、テストデータでは高いエラー率を示す.

• 低分散：トレーニングデータセットの変更に伴って、目的関数の推定値に小さな変更を加えることを提案する.
• 高分散：トレーニングデータセットの変更に伴って、ターゲット関数の推定値に大きな変更があることを示唆する.

教師付き機械学習アルゴリズムは、低バイアスと低分散を達成した結果、優れた予測性能を達成する.

最尤推定 vs. MAP推定

最尤推定とMAP推定の特徴

• データ（分布）を固定してパラメータを動かす <-> 普通：
• 尤度関数を最大化するθ探し（argmax）
• ベイズの定理に比べ, 事前確率(データを手に入れる前に想定していた確率）を無視

最尤推定

事後分布は無限に尖った確率分布であり、事前分布は無限に平坦な確率分布であると仮定したもの

特徴:

• 事前情報（確率変数の分布）のみによる推定

MAP推定

最尤法に対して, 事後分布を無限に尖った確率分布であると仮定したもの

特徴:

• 最尤法に事後情報を加えた推定

信頼区間と区間推定

• 区間推定：分散が既知な場合

パラメータとは？

パラメータとは、母集団全体の記述的測度です。 ただし、母集団全体を測定することができないため、通常その値は不明です。したがって、母集団からランダムサンプルを抽出してパラメータ推定値を取得できます。統計分析の目的の1つは、母集団パラメータの推定値と、これらの推定値に付随する誤差の量を得ることです。これらの推定値は、サンプル統計量とも呼ばれています。

パラメータ推定値には次のものがあります。 点推定値は、パラメータの最も可能性がある単一の値です。たとえば、母平均（パラメータ）の点推定値はサンプルの平均値（パラメータ推定値）です。 信頼区間とは、母集団パラメータの含まれる可能性が高い値の範囲です。

相関関係 vs 共分散

2つの確率変数間の依存性も測定する.

相関関係

2つの変数がどれだけ強く関連しているかを測定する.

共分散

　2つの変数の変化が他の変数の対応する変化によって逆数になる、一対の確率変数間の系統的な関係を説明する.

4. 仮説検定 from 推測統計学

帰無仮説 and 対立仮説

• ある一つの変数が他の一つの変数，もしくは一群の変数と関係がないとする仮説．
• あるいは二つ以上の母集団の間の差がないとする仮説．

これが成立するならば，得られた結果は偶然によって支配されたと予想される結果と違わないことになる．

仮説検定は、母集団について行われた分析結果の妥当性を検証する. 帰無仮説は、仮説と指定された母集団がサンプリングまたは実験誤差のために有意差がない場合の状況です.

• 検定
  • 帰無仮説:
  • 有意水準:

P値（優位確率）と有意水準

帰無仮説が正しいとき、誤って帰無仮説を棄却（否定）してしまう確率

仮説検定を実行するとき、p値によって推定結果の信頼性を判断する.

有意水準

統計的仮説検定において第一種の過誤を犯す確率のことで、P値の小ささの基準.P値が有意水準よりも小さい場合は帰無仮説は棄却される.

T検定とZ検定

パラメトリック検定 vs. ノンパラメトリック検定

　サンプルデータの分布が明らかになっているorこちらで仮定している場合か, 否か.

5. ベイズ統計学

ベイズの定理

結果から原因を求める

数式

1. 条件付き確率 式１：p(Y|X) = p(X, Y) / p(X) X=条件
2. XとYを交換　入れ替えても成り立つ 式２：(X|Y) = p(X, Y) / p(Y)
3. 式１を変形 式３：p(X, Y) = p(Y|X) * p(X)
4. 式２に式３を代入：(X|Y) = p(Y|X) * p(X) / p(Y)
5. 確率の乗法定理

• ベイズの定理 = 条件付き確率 + 乗法定理（加法定理）
• 確率分布
  • ベイズ定理() = 最尤法 + 事後情報
  • 最適化

独立と排反

• AとBは同時に起こらない
• 条件付き確率は排反条件

6. Advanced Topic

次元削除

• PCA
• SVD
• LDA
• Word2Vec

正則化

ペナルティー項と呼ばれ、損失関数を最小化を実行しようとしたときに、第一項だけを小さくできたとしても、第二項が大きくなるのはダメというペナルティーを与えて、wの値を考えなおさせることができる.

L1正則化（ラッソ）

単に不要なパラメータを削りたい（次元・特徴量削減）という時によく使われる

L1正則化(リッジ)

過学習を抑えて汎化された滑らかなモデルを得やすいことが知られている

交差エントロピー誤差

情報理論において2つの確率分布の間に定義される尺度 - 引用: wikipedia

モデルの出力が、観測値に近ければ近いほど損失関数の値は小さくなっていく. だから、損失関数の値が最小になる出力となるように、重みやバイアスなどのパラメータを調整すれば, 正確な判断ができるニューラルネットワークを作れる.

KL Divergence　カルバック・ライブラー情報量

隠れマルコフモデル

時系列データにおける統計学

Confidence Intervals vs. Prediction Interval

References

• How To Ace Data Science Interviews: Statistics
• Top 45 Data Science Interview Questions You Must Prepare In 2019
• Statistics Interview Questions, Useful And Most Asked